In the course of playing around with code to run the Büchi automata for the LTL constraint I’m adding to Pandamator, I realized that all that could be packaged into a nifty little feature for checking object evolution (or evolution of whole systems, for that matter). Enter LtlChecker, a library to help you apply the power of LTL to your imperative programs. Its only dependency is SPOT.fs from the Pandamator project, whose job is to execute SPOT and parse the automaton it produces. And SPOT itself, of course. I have took the easy way out regarding how SPOT is found: it must be in the path. Please note that cygwin1.dll must be on the path as well, for SPOT to be invoked.
SPOT.fs can be found in the SVN repository and, in any case, I have described it in the relevant post. I will focus on the new code, LtlChecker.fs. In an attempt to make it more C#-friendly, I have used Dictionary instead of Map.
Here’s a simple usage scenario, with which I will demonstrate how it works and I’ll present the implementation later.
type _test_struct = {
mutable x: int
}
let _unit_test () =
let obj = { new _test_struct with x=0 }
let dic = new Dictionary<string,System.Func<bool>> ()
dic.Add("p0",(fun () -> obj.x > 0))
dic.Add("p1",(fun () -> obj.x > 0))
let con = create_constraint "G(p0 -> G p1)" dic
let i0 = init con
obj.x <- 1
let i1 = next i0
obj.x <- 0
let i2 = next i1
obj.x <- 1
let i2b = next i1
(i0,i1,i2,i2b)
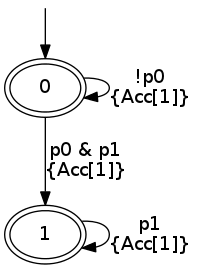
I have actually traced two diverging paths, for the constraint G(p0 -> G p1), where p0 and p1 both mean “property x of the test object is > 0”. The constraint can be translated as “once x becomes > 0, it never becomes zero again”.
Calling create_constraint creates an LtlConstraint, which is used to initialize the constraint checking. Calling init on it, evaluates propositions at the initial state and gives you back a ConstraintResult, which is what you’ll be examining throughout the constraint checking. The relevant property you should be looking at is status, an enumeration that tells you if the constraint has failed (Failed), if the system is at a state where it can be terminated with the constraint being fulfilled (CanTerminate), or if the system cannot be terminated now because the constraint awaits fulfillment (CannotTerminate).
Let’s look at it in practice. Here’s what i0 looks like.
{currentstates = [{state = 0;
accepting = true;}];
status = CanTerminate;
ltlconstraint =
{automaton =
{acccondnum = 1;
states =
[|{initial = true;
transitions =
[{endstate = 1;
acccond = [0];
guard = Bin (And,Prop "p1",Prop "p0");};
{endstate = 0;
acccond = [0];
guard = Not (Prop "p0");}];};
{initial = false;
transitions = [{endstate = 1;
acccond = [0];
guard = Prop "p1";}];}|];};
propositions =
dict
[("p0",
System.Func`1[System.Boolean] {Method = Boolean Invoke();
Target = LtlChecker+_unit_test@87;});
("p1",
System.Func`1[System.Boolean]
{Method = Boolean Invoke();
Target = LtlChecker+_unit_test@88-1;})];};}
Status is CanTerminate, because x is still 0. In i1, status is still CanTerminate, and the current state is now state 1.
In i2, where x has gone to being 0 again, the status is Failed! That’s what one would expect.
In i2b, which is an alternative path from i1 but with x continuing to be bigger than 0, the status remains CanTerminate.
That’s is. A small facility to apply temporal logic in the evolution of mutable systems! In fact, you can apply it to any timeseries.
Nota Bene: I cannot guarantee that my interpretation of how running a Büchi automaton is done, is correct. It might happen that what works for the LTL expression above, might not work for some other expression. If I find problems (and manage to overcome them), I will update the code on SVN.
Here’s the code itself (it can also be found in the SVN repository, in project LtlChecker.
module LtlChecker
open System.Collections.Generic
open SPOT
type LtlConstraint = {
automaton: BuchiAutomaton;
propositions: Dictionary<string,System.Func<bool>>;
}
type ConstraintStatus = Failed | CanTerminate | CannotTerminate
type ConstraintState = {
state: int;
accepting: bool;
}
type ConstraintResult = {
currentstates: ConstraintState list;
status: ConstraintStatus;
ltlconstraint: LtlConstraint;
}
let rec execute_logexp (propositions:Dictionary<string,System.Func<bool>>) (exp:LogicExpr) =
match exp with
| Const v -> v
| Not e -> not (execute_logexp propositions e)
| Bin (o, x, y) ->
let lx = execute_logexp propositions x
let ly = execute_logexp propositions y
match o with
| And -> lx && ly
| Or -> lx || ly
| Impl -> execute_logexp propositions (Bin(Or,Not(x),y))
| Equiv -> execute_logexp propositions (Bin(Or,Bin(And,x,y),Bin(And,Not(x),Not(y)))) // (x and y) or (not x or not y)
| Xor -> execute_logexp propositions (Bin(And,Bin(Or,x,y),Not(Bin(And,x,y)))) // (x or y) and not(x and y)
| Prop p ->
let rc = propositions.[p]
rc.Invoke()
let create_constraint (ltl:string) (propositions:Dictionary<string,System.Func<bool>>) =
let ba = ltl2ba ("'"+ltl+"'")
{ new LtlConstraint
with automaton = ba
and propositions = propositions
}
let do_transitions (state:int) (con:LtlConstraint) =
let states = con.automaton.states.[state].transitions
|> List.filter (fun t -> execute_logexp con.propositions t.guard)
|> List.map (fun t -> { new ConstraintState with state=t.endstate and accepting=t.acccond.Length>0 }) //Finite paths cannot work with more than one accepting condition
states
let states_to_result (nextstates:ConstraintState list) (con:LtlConstraint) =
let status =
if nextstates.Length = 0 then
Failed
elif nextstates |> List.exists (fun s -> s.accepting) then
CanTerminate
else
CannotTerminate
{ new ConstraintResult
with currentstates=nextstates
and ltlconstraint=con
and status=status
}
let init (con:LtlConstraint) =
let initialstate = con.automaton.states |> Array.findIndex (fun st -> st.initial)
let nextstates = do_transitions initialstate con
states_to_result nextstates con
let next (res:ConstraintResult) =
let nextstates = res.currentstates |> List.map (fun s -> do_transitions s.state res.ltlconstraint) |> List.fold (@) []
states_to_result nextstates res.ltlconstraint